|
|
4 years ago | |
|---|---|---|
| .. | ||
| code | 4 years ago | |
| images | 4 years ago | |
| README.md | 4 years ago | |
README.md
第四次作业报告
一、多分类问题方法
通过查阅资料了解到,使用逻辑回归处理多分类问题常用的有三种方法,第一种是One-Vs-All,先把其中一类(A)看成一组,剩下的都看成一组,这样交给二分类的逻辑回归程序后,可以训练出识别A类的特征,剩下的几类继续照前面的方法训练;第二种是One-Vs-One,将多类两两一组组合,在每一组中使用二分类程序进行训练,训练完在使用时,将给定数据分别使用这些二元分类器,最后投票,票数哪个多就归哪类;第三种是Softmax方法,它可以让多输出映射到[0, 1]区间内,并使它们映射后值的和为1。Softmax方法中对一个测试样本得到的属于各类别的概率和一定为 1,而多个二分类器策略中,不管是 One-Vs-All、One-Vs-One策略,一个样本在多个二分类器上得到的概率和不一定为 1。因此当分类之间是互斥的情况下(e.g 数字手写识别、动物识别),通常采用 Softmax方法;而目标类别不是互斥时(e.g 华语音乐、流行音乐、重金属音乐等)则采用多个二分类器策略进行预测。
本次作业中要求进行手写数字识别,适合采用Softmax方法,故接下来就对Softmax的原理以及公式进行解释和推导。
二、Softmax方法原理
Softmax函数的公式如下:
g(z_i)=\frac{e^{z_{i}}}{\sum\limits_{j=1}^{n} e^{z_{j}}}
其中,n表示多个输出或类别数,z_j为第j个输出或类别的值,i表示当前需要计算的类别。从上述公式中可以看出,Softmax函数的计算结果落在[0,\ 1]中,且所有类别的Softmax函数值之和等于1。
在输入到输出之间引入一层函数映射,取\mathbf{\Theta}^T\cdot\mathbf{x}+\mathbf{b}=\mathbf{z},其中\mathbf{\Theta}=[\theta_1,\ \theta_2,\ ,...,\ \theta_n]为权重系数,\theta为权重向量,\mathbf{x}为输入向量,\mathbf{z}为输出向量,则Softmax函数可以写成:
g(z_i)=g(\theta_i^T \mathbf{x}+b_i)=\frac{e^{\theta_i^T\mathbf{x}+b_i}}{\sum\limits_{j=1}^{n} e^{\theta_j^T \mathbf{x}+b_j}}=h_{\theta_i, b_i}(\mathbf{x})
构造似然函数,若有m个训练样本:
\begin{aligned}
L(\Theta;\mathbf{b})&=p(\mathbf{y}|\mathbf{X};\Theta,\mathbf{b}) \\\\
& = \prod\limits_{i=1}^{m} p(y^{i}|\mathbf{x}^{i};\Theta,\mathbf{b}) \\\\
& = \prod_{i=1}^m h_{\theta_i,b_i}(\mathbf{x})
\end{aligned}
对似然函数取对数,转换为:
l(\Theta,\mathbf{b})=log(L(\Theta),\mathbf{b})=\sum\limits_{i=1}^m log(h_{\theta_i,b_i}(\mathbf{x}))
对log(h_{\theta_i,b_i}(\mathbf{x}))对z_k求导得到:
\frac{\partial{log(h_{\theta_i,b_i}(\mathbf{x}))}}{\partial{z_k}}=\begin{cases}
1-h_{\theta_k,b_k}(\mathbf{x}) & \text{ if } k=i \\\\
-h_{\theta_k,b_k}(\mathbf{x}) & else
\end{cases}
转换后的似然函数对\theta求偏导,在这里我们以只有一个训练样本的情况为例:
\begin{aligned}
\frac{\partial}{\partial\theta_k}l(\Theta,\mathbf{b})&=\frac{\partial l(\Theta,\mathbf{b})}{\partial{z_k}}\cdot \frac{\partial z_k}{\partial \theta_k} \\\\
&=(y_k-h_{\theta_k,b_k}(\mathbf{x}))\mathbf{x}
\end{aligned}
对偏置项b求偏导与上述类似:
\frac{\partial}{\partial b_k}l(\Theta,\mathbf{b})=y_k-h_{\theta_k,b_k}(\mathbf{x})
上式中y_k的表达式如下:
y_k=\begin{cases}
1 & \text{ if } k=i \\\\
0 & else
\end{cases}
此时,我们就可以写出最大化似然函数的更新方向,\theta_k与b_k的迭代表示为:
\theta_k=\theta_k+\eta(\sum\limits_{i=1}^{m}(y_k-h_{\theta_k,b_k}(\mathbf{x}^i))\cdot \mathbf{x}^i)
b_k = b_k+\eta (\sum\limits_{i=1}^{m}(y_k-h_{\theta_k,b_k}))
其中\eta为学习率,可以看到,当输出向量的维度等于2时,即二分类时,上式与二分类中权重向量的迭代公式相等。
三、运行结果
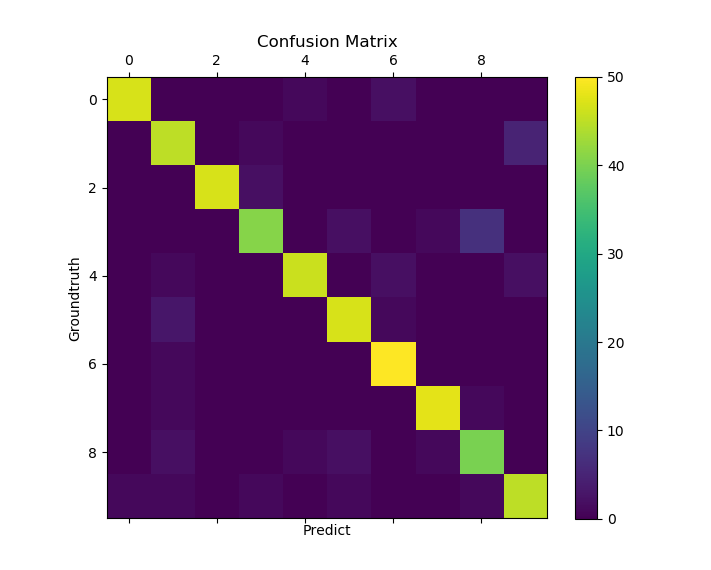
使用的数据是sklearn中的digital数据,其每一个样本由64个像素组成,输出结果是0-9中的一个数。由于输入和输出都是一个高维向量,最后结果采用confusion matrix可视化出来,其主对角线上的个数为预测正确的数目,其余位置上的元素为预测失败的样本个数。
由于sklearn中的digital数据有1700多个样本数据,我们将前1200多个样本作为训练数据,最后500个作为测试数据,分别采用自己实现的softmax回归方法以及sklearn内置的OVR多分类方法进行训练并预测。
softmax回归的confusion matrix:
softmax回归在训练数据上的预测精度以及在测试数据上的预测精度为:
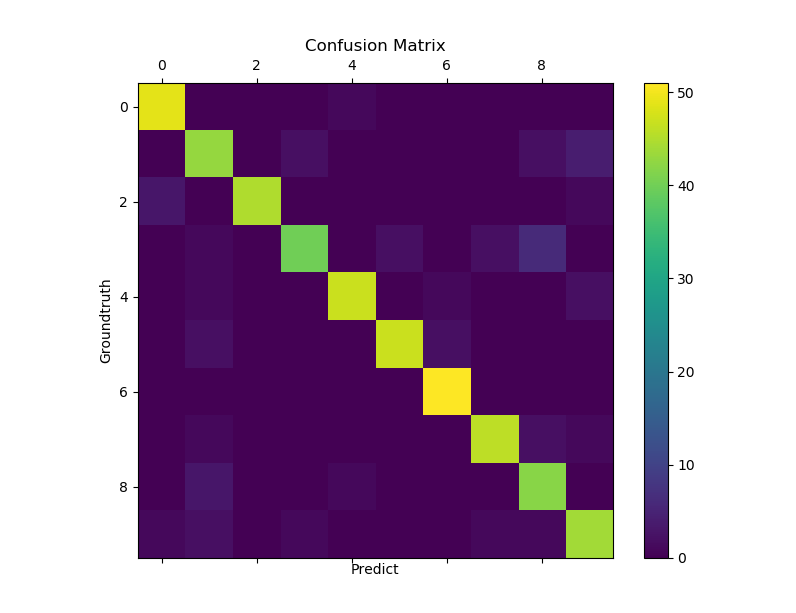
使用sklearn内置的多分类方法运行结果的confusion matrix:
sklearn内置的多分类方法在训练数据上的预测精度以及在测试数据上的预测精度为:
从上面的运行结果中来看,自己实现的softmax方法以及sklearn内置的多分类方法最后在测试数据上的预测精度都达到了0.9以上,二者的差距非常的小。